
| Home | People | Research | Publications | Demos |
| News | Jobs |
Prospective
Students |
About | Internal |

| Learning Mixture Hierarchies | |
|
|
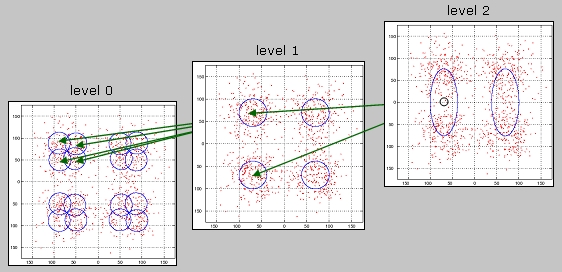
There are many problems in learning, perception, and signal processing that have inherent hierarchical structure. For example, in human and machine vision objects are usually naturally grouped into perceptual hierarchies, in signal processing there are many processes which are best analyzed at multiple resolutions, in machine learning hidden variables are frequently well modeled by hierarchical cause-effect relationships, and so forth. When developing models for hierarchical processes, it is usually a good idea to encode hierarchical constraints in the models themselves, as this significantly simplifies the learning process. There are two main approaches for learning hierarchical models. Bottom-up procedures start by learning the models for simple classes at the leaves of the hierarchy (which is represented as a tree) and progress up to the more complex classes at the top. Top-down procedures learn complex models first, and then refine them in a divide-and-conquer type of strategy. This project addresses the problem of density estimation under hierarchical constraints. The starting point is the well known observation that most densities can be well approximated by mixture models. The question is then how to estimate the parameters of mixture hierarchies. A variety of approaches are available in the literature, e.g. in the area of clustering, for solving the problem in a top-down fashion. This typically involves learning a mixture with few components, then splitting those components to obtain a finer-grain mixture, and recursively proceed until a very detailed model is obtained. Examples of such approaches include tree-structured vector quantizers, incremental EM learning by centroid splitting, deterministic annealing, etc. One significant limitation of this framework is that there is no efficient re-use of computation. Since the progression is from a coarser to a finer representation of the data, all the data-points have to be revisited at each hierarchical learning stage. The opposite view of bottom-up learning is implemented by so-called agglomerative clustering methods. These start at the bottom, by grouping a set of points and replacing them by a new cluster representative. Cluster representatives are then merged, and the process iterated until an entire tree is built. These approaches are computationally efficient, in the sense that once the representative for a given cluster is found all subsequent computations are based on that representative, the original points no longer need to be considered. This means that the learning of a given level fully exploits the previous computation. In result, computation decreases exponentially as learning progresses up the tree. The main limitation of these procedures is, however, that a single representative can be a very poor approximation to the cluster it represents. Hence, the quality of the estimates can degrade quickly as one moves up the tree. This project addresses the problem of bottom-up learning of mixture hierarchies, where a complete density (not just a representative) is kept at each node of the tree and where the estimation of the parameters of the density associated with a node takes into account the entire density of the children nodes. The problem has been solved for Gaussian mixture hierarchies, through the derivation of an hierarchical extension of EM that only requires knowledge of the parameters of the levels below in order to learn the parameters of a given node. The algorithm is therefore extremely efficient, combining the reduced complexity of agglomerative clustering with the ability of top-down procedures to produce accurate density estimates at all levels of the hierarchy. Current research focus on the use of the algorithm to solve the problem of "learning classifiers from classifiers". For example, given a collection of image classifiers for low-level concepts such as sky, grass, people, etc. how does one derive classifiers for higher-level semantics (such as deciding if an image contains an indoor or outdoor scene) without having to revisit all the points in the original training set? This formulation has been shown to be quite useful for problems such as image indexing, or the design of semantic classification hierarchies. |
|
| Selected Publications: |
|
| Demos/ Results: |
|
| Contact: | Nuno Vasconcelos |
![]()
©
SVCL