
| Home | People | Research | Publications | Demos |
| News | Jobs |
Prospective
Students |
About | Internal |

| Probabilistic Kernel Classifiers | |
|
|
|
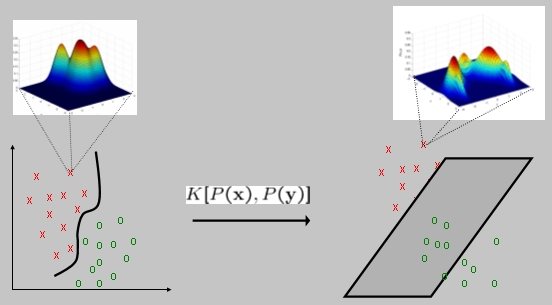
In statistical learning, there are two basic methods to design a classifier. The first, usually referred to as "discriminant", models the decision boundaries between the different classes. Examples of classifiers in this group include neural networks, the perceptron, or support vector machines (SVM). The last decades have witnessed significant advances in the theory of these classifiers, which have lead to the development of so-called "large-margin" classifiers. SVMs are probably the most popular architecture in this class. Roughly speaking, the basic idea is to consider two linearly separable classes and find the boundary hyper-plane that maximizes the distance to the closest point on each side (the margin). The fact that the boundary is usually not an hyper-plane is addressed by the introduction of a function known as the "kernel", which is equivalent to solving the linearly separable problem in an alternative, high-dimensional, feature space (where the assumption of linear separability is much more sensible). There are also extensions to handle non-separable problems, as well as problems with more than two classes. While popularized in the context of the SVM classifier, this "kernel trick" has more recently been shown to be useful for a wide range of problems. The second major method of classifier design is based on so called "generative" models. These are models for the probability distributions of each of the classes, that can be transformed into a classifier through the application of Bayes rule (the resulting classifier is the so-called "plug-in" classifier). This family includes most of the classical classifiers, e.g. the Gaussian classifier, and classifiers based on maximum-likelihood or maximum-a-posteriori probability rules. Many popular architectures for image and speech classification belong to this family (e.g. speech recognizers based on hidden Markov models, image classifiers that rely on Markov random field modeling, etc.). The generative route to classifier design is, in many ways, more appealing than the discriminant one: it can take advantage of any prior knowledge about the structure of the classification problem (e.g. by the selection of appropriate probabilistic models) to build better classifiers, it allows for modular solutions where complex problems are decomposed into simpler ones whose solutions are then integrated via statistical inference (e.g. Bayesian networks and belief propagation), it can handle problems for which it is not clear how to design discriminant classifiers (e.g. on speech or DNA classification different classes may produce strings of different lengths; while it is not clear how to define a direct distance between them it is relatively straightforward to measure likelihoods when the classes are abstracted into hidden Markov models), and it can rely on Bayesian inference to implicitly constrain classification boundaries. On the other hand, estimating densities is a harder problem than determining classification boundaries directly and discriminant methods have better generalization guarantees, which usually translate into better practical classification performance. This project explores the question of the design of classifiers that combine the best properties of both the generative and discriminant worlds. This is achieved by making the kernels, used in discriminant learning, functions of probabilistic models for the class densities. These are known as "probabilistic kernels" and build on the interpretation of the kernel as a distance function between data points on some, possibly non-linear, manifold. Instead of measuring distances between the points themselves, probabilistic kernels first abstract the classes into suitable probabilistic models and them measure the distance between such models. Besides introducing a new family of probabilistic kernels, based on information-theoretic distances such as the Kullback-Leibler, Jensen-Shannon, or Renyi divergences, this project has also shown that probabilistic kernels are particularly well suited for multimedia (vision and speech) classification problems, due to their support for localized representations. Such representations are much more robust to problems like invariance to image transformations or occlusion than the standard global SVM representation that treats each object as a template. |
|
| Selected Publications: |
|
| Demos/ Results: |
|
| Contact: | Antoni Chan, Pedro Moreno, Nuno Vasconcelos |
![]()
©
SVCL