|
In this page we discuss the neurophysiological plausibility of the proposed
bottom-up
discriminant saliency detector (DSD). We first give a brief overview
of the detector, and then discuss the connections to the neurophysiology
of early visual processing.
Discriminant center-surround saliency detector
Bottom-up saliency is defined as a center-surround classification problem.
At every image location, saliency is equated to the power of a set of Gabor-like
features to discriminate between the stimuli at that location (the center) and
those in a surrounding window (the surround). Discrimination is measured by
the mutual information between features and the center-surround label.
Natural image statistics are exploited to derive a computationally parsimonious
mechanism. The implementation of the detector is presented in Figure 1:
the image is first decomposed into various feature maps, such as color, intensity,
and orientation. Each feature map is then subject to a center-surround operation,
to generate a feature saliency map (Figure 2) which measures feature
discrimination (mutual information) at each image location. A global saliency map
is finally computed by pooling all feature-based saliency maps.
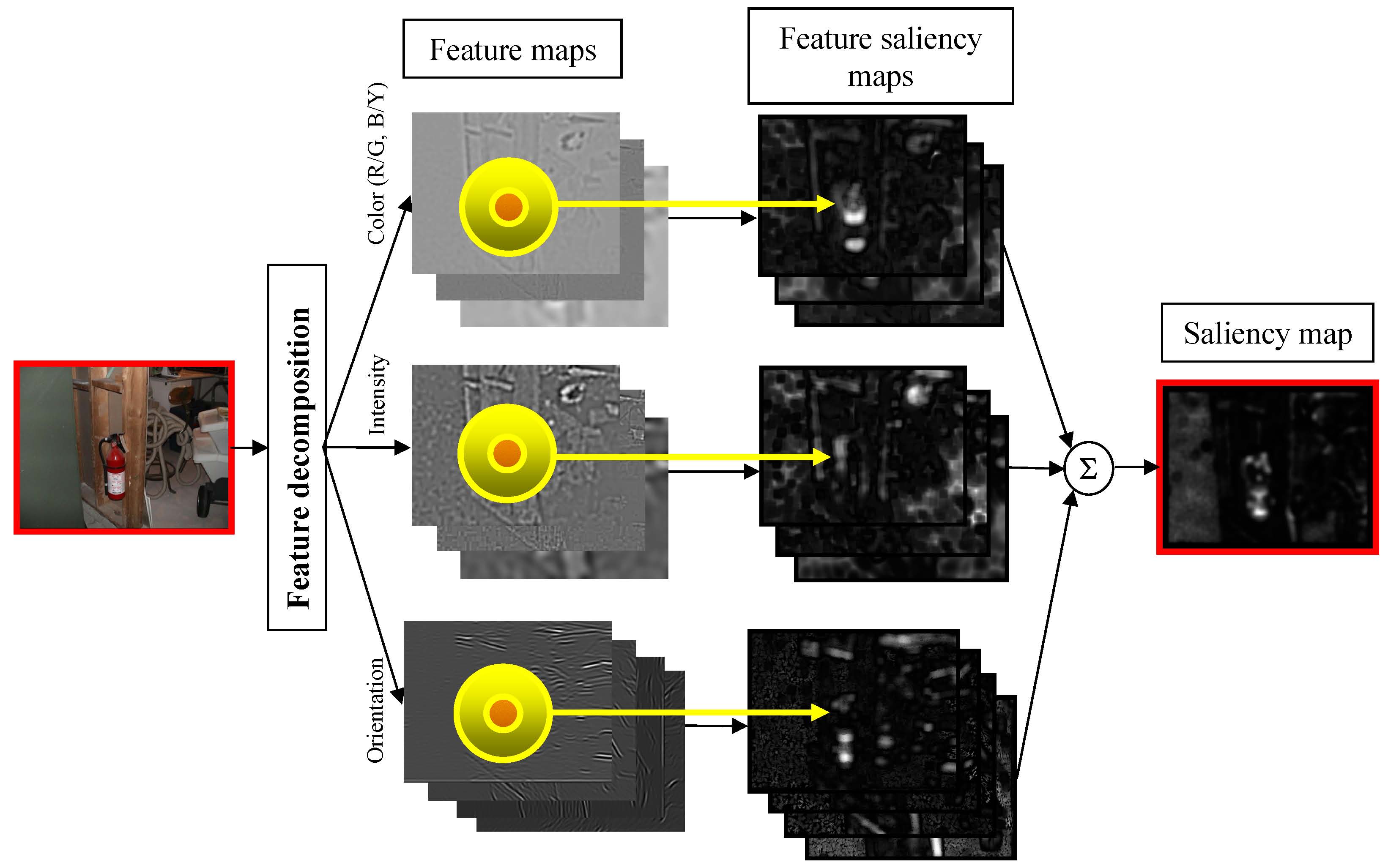
Figure 1: The bottom-up discriminant saliency detector.

Figure 2: Illustration of discriminant center-surround saliency operation.
Consistency with the standard neural architecture of V1
It is well known that the application of band-pass filters to natural images produces
features whose statistics comply with the generalized Gaussian distribution (GGD).
For these features, all computations of discriminant saliency can be implemented by
the following neural network, which consists of a combination of simple and
complex cells, and is fully compatible with the standard neural architecture of V1.
The network has three layers: 1) the first layer consists of linear filtering and
(differential) divisive normalization, and is consistent with the divisive normalization
model of simple cells; 2) the second layer recitifies the output of the first layer by
a quadratic nonlinearity and pools such outputs in a neighborhood, akin to the
energy model of complex cells; 3) a third layer, which performs pooling across
feature channels, and can be mapped into a cortical column.
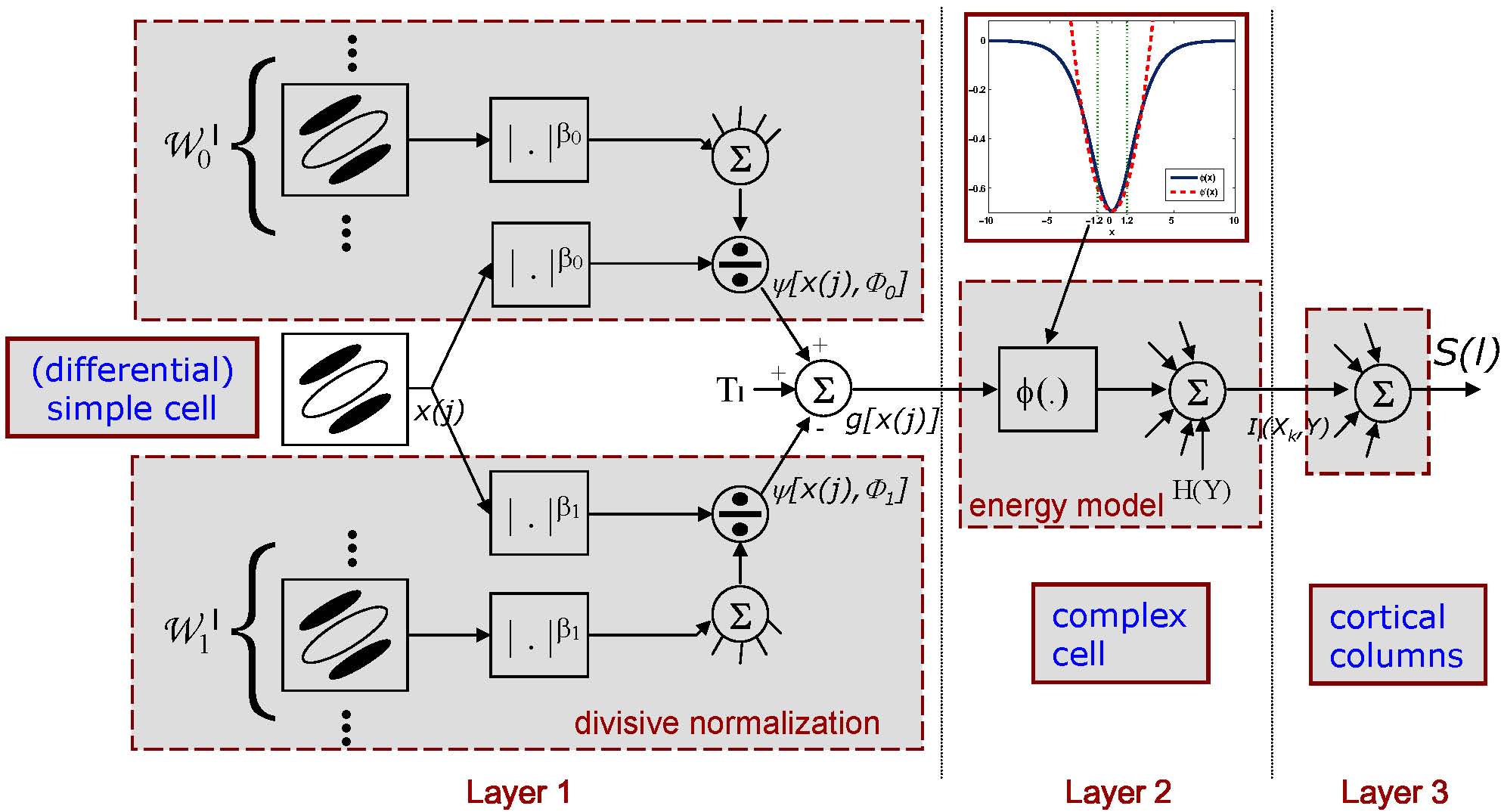
Holistic functional justification, and statistical inference, in V1
In addition to proving the physiological plausibility of discriminant saliency,
the parallel between the above network and the standard architecture of V1
also offers a holistic functional justification for V1: that it has the capability to
optimally detect salient locations in the visual field, when optimality is
defined in a decision-theoretic sense and certain approximations are allowed,
for the sake of computational parsimony. It can also be shown that,
for stimuli compliant with natural image statistics, there is a rich set of explicit
correspondences between the components of the discriminant saliency network
and the fundamental operations of probabilistic inference. In particular, all
components (cells) of the standard V1 architecture have a statistical
interpretation, and this interpretation covers the three fundamental
operations of statistical inference: probability inference, decision rules, and feature
selection. The correspondence is as follows
| simple cells |
- |
assess probabilities. |
| differential simple cells |
- |
implement decision rules. |
| complex cells |
- |
feature detectors that evaluate mutual information. |
The fundamental operation of statistical learning, parameter
estimation, is also performed within the architecture, through
the divisive normalization subjacent to all computations.
|





![]()